Image processing for materials characterization (ICIP 2014, special session)

ICIP 2014, the IEEE International Conference on Image Processing, will take place in Paris (la Défense, to be honest) during 27-30 October 2014. The twenty special sessions have been announced (see below).
One is devoted to the exciting field of Materials science: "Image processing for materials characterization", with one introductory and five invited papers.

ICIP 2014 Special Session

"Image processing for materials characterization"

CLICK THE PICTURE FOR THE DEDICATED PAGE

 The deadline for paper submission is 14 February 2014. We encourage interested authors to submit as many papers as possible around this topic (ICIP 2014 submission information), and to warn one the special session organizers. Beware: the existence of the special session on "Image processing for materials characterization" does not grant, by no mean, acceptance or even higher odds to the main conference tracks.

• Maxime Moreaud (@IFPEN dot fr, with a dot in the space)
• Laurent Duval (@IFPEN dot fr, with a dot in the space)
• Camille Couprie (@IFPEN dot fr, with a dot in the space)
• Jesus Angulo (@ensmp dot fr, with a dot in the space)
• Dominique Jeulin (@ensmp dot fr, with a dot in the space)
• H Talbot (@esiee dot fr, with a dot in the space)

Context

Scanning electron microscopy (SEM): or Mr. Jack (c) F. Moreau, IFPEN

A microscopic Mister Jack (left) announces the present conference/special session.  Materials science is evolving from materials discovered in Nature by chance to designed materials [1], that repair themselves, adapt to their environment, capture and store energy or information, help elaborate new devices, etc. Materials are now designed from scratch with initial blueprints, starting from atoms and molecules,   as more traditional for buildings or electronic circuits. This evolution, at the confluence of science, technology, and engineering [2], is driven by the synergy of materials science and physics, mechanics, chemistry, biology and engineering, with image processing  taking part in this challenge [3]. Indeed, the possibility of designing, analyzing and modeling materials from images (or generally two- or three-dimensional modalities) reveals important contributions to this field. The  appearance of materials  changes significantly with imaging techniques, depending  on the scale of analysis, imaging settings, physical properties and preparation of materials. Understanding these aspects turns out to be crucial for material analysis and modelization.

In particular, we face challenges regarding the characterization of the physical assembly process of materials, the formation process of images, of imaging techniques interacting with materials (geometry, transmission, illumination, reflection, scattering). Answering these questions is important to separate the material appearance from its intrinsic morphology and properties. Additionally, materials science approaches may inspire novel image processing techniques.

We make an analogy between images and statistical mechanics systems. Pixel gray levels and the presence and orientation of edges are viewed as states of atoms or molecules in a lattice-like physical system.

By gathering researchers of complementary expertise, from image feature extraction to image simulation, this special session proposal will allow us to report on recent progresses performed and emerging trends in material analysis and modelization through image processing. By attracting an audience with diverse backgrounds, this proposal aims at catalyzing a new community around this exciting new area for the image processing crowd. The special session topics will be publicized, to encourage  additional submissions to the main ICIP session tracks.

Scope

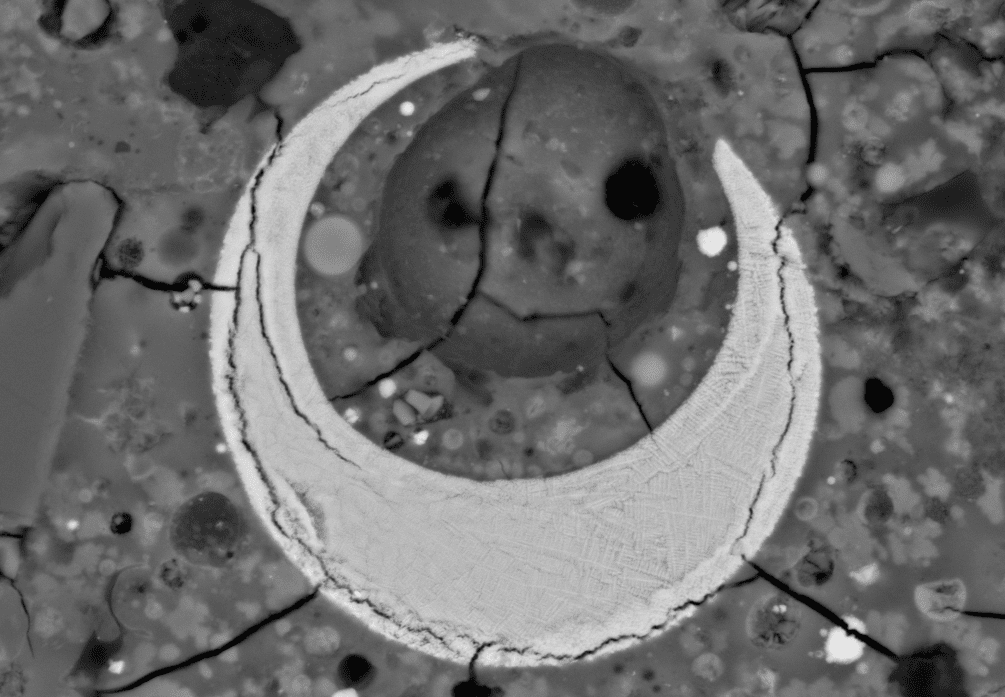
Scanning electron microscopy (SEM): Catalyst section with cracks and inclusions.

This special session aims at showing some relevant problems in material characterization that can be addressed with classical or advanced methods of signal and image processing. It will be introduced by a tutorial presentation, given by the organizers, who will offer a large overview of some of the issues that may be addressed in this application domain, such as dealing with different modalities (optical, scanning or transmission electron microscopy; diffractometry; spectrometry; surface analysis instrumentation...) and applications (porous, fibrous and hard materials; membranes, surfaces and interfaces; clean energy and information storage; chemistry and catalysts; geology; forensics; bio-inspired materials and biomedical  [4]). For illustrating and to widen the points of view of the tutorial, the five invited papers of the session address some of these challenges by employing various methods, e.g. restoration; segmentation; mathematical morphology; texture analysis [5]; multiscale and directional features extraction; color and multispectral processing; stochastic models [6]. Organizing committee information is given on the next page, followed  by invited authors' contributions, in shape of  expanded abstracts, preliminary results and references. The proposal is concluded by a discussion on the authors' expertise.

Topics of interest include (but are not limited to):

• Modalities: optical, scanning or transmission electron microscopy; diffractometry; spectrometry; surface analysis instrumentation…
• Approaches: restoration; segmentation; mathematical morphology; texture analysis; multiscale and directional features extraction; color and multispectral processing; stochastic models; rendering; sparse sensing…
• Applications: porous, fibrous and hard materials; membranes, surfaces and interfaces; clean energy and information storage; chemistry and catalysts; geology; forensics; bio-inspired materials and biomedical

Thanks to:
Nuit Blanche: Novel meetings: Image processing for materials characterization (ICIP 2014, special session), Spin Glass and Beyond: An old tool for new problems, ITWIST'14 deadline extended 
IFPEN

The list of ICIP 2014 special sessions:
SS-1: Variational and Morphological Optimizations: A Tribute to Vicent Caselles
Organizers: Jean Serra, Guillermo Sapiro, and Philippe Salembier

SS-2: Learning Image Features to Encode Visual Information
Organizers: Jesús Malo, Javier Portilla, and Joan Serra-Sagristà

SS-3: Plenoptic Imaging (Capture, Representation, Processing, and Display)
Organizers: Mårten Sjöström and Atanas Gotchev

SS-4: Photon-Limited Image Reconstruction
Organizers: Charles Deledalle and Joseph Salmon

SS-5: Hyperspectral Image Processing
Organizers: Saurabh Prasad and Jocelyn Chanussot

SS-6: Compact Feature-Based Representation of Visual Content
Organizers: Giuseppe Valenzise and Marco Tagliasacchi

SS-7: Advances in Optimization for Inverse-Imaging Problems
Organizers: Jalal Fadili and Gabriel Peyré

SS-8: Quality of Experience in 3D Multimedia Systems
Organizers: Janko Calic, Philippe Hanhart, Patrick Le Callet, and Alexandre Pereda

SS-9: Advances in Astronomical Signal and Image Processing
Organizers: Jérôme Bobin and Yves Wiaux

SS-10: Image Processing for Materials Characterization
Organizers: Maxime Moreaud, Laurent Duval, Camille Couprie, Dominique Jeulin, Jesús Angulo, and Hugues Talbot

SS-11: Realistic 3D in Interactive Virtual Worlds
Organizers: Julie Wall and Ebroul Izquierdo

SS-12: Electron-Microscopy Image-Processing Problems and Applications in Biology: From Structure to Dynamics
Organizers: Slavica Jonic and Carlos Oscar Sanchez Sorzano

SS-13: Advances in Facial Morpho-Functional Sign Recognition and Analysis
Organizers: A. Enis Cetin, Sara Colantonio, and Bogdan J. Matuszewski

SS-14: Synthetic Aperture Radar Imaging
Organizers: Daniele Riccio

SS-15: 3D Data Security
Organizers: William Puech and Adrian Bors

SS-16: 3D Multimedia Experience Over the Future Internet
Organizers: Safak Dogan, Erhan Ekmekcioglu, and Ahmet Kondoz

SS-17: Efficient Design of HEVC Video-Codec Implementations
Organizers: Vivienne Sze

SS-18: Behavior Imaging
Organizers: Séverine Dubuisson, Jean-Marc Odobez, and Mohamed Chetouani

SS-19: Image Processing for the Detection of Road-Surface Degradations
Organizers: Paulo Lobato Correia and Henrique Oliveira

SS-20: Privacy-Preserving Multimedia Content Analysis: Privacy by Design and Social-Impact Analysis
Organizers: Atta Badii, Touradj Ebrahimi, Jean-Luc Dugelay, Ebroul Izquierdo, Thomas Sikora, Leon Hempel, Christian Fedorczak, and Diego Fernandez Vazquez

Géométrie espace-temps

Une jolie série historique sur la géométrisation progressive du monde observé, par les philosophes et les scientifiques, en série d'épisodes de 10 minutes.

La géométrie de l'espace et du temps  1

Introduction : physique et géométrie, naissance de l'esprit scientifique (de la narration mythique à l'explication).

La géométrie de l'espace et du temps  2

Une vision du monde totalement géométrisée. L'harmonie et la symétrie, le cosmos, solides de Platon ou polyèdres réguliers, mis en relations avec les éléments, précurseurs des groupes de symétries. "Planète" veut dire "voyageur". Le dodécaèdre, plus proche de la sphère en symétrie, sert à représenter un cinquième élément.

La géométrie de l'espace et du temps  3

La géométrie de l'espace et du temps  4

La géométrie de l'espace et du temps  5

La géométrie de l'espace et du temps  6

La géometrie de l'espace et du temps  7

La géometrie de l'espace et du temps  8

La géometrie de l'espace et du temps  9

La géometrie de l'espace et du temps  10

La géometrie de l'espace et du temps  11

A Primal-Dual Proximal Algorithm for Sparse Template-Based Adaptive Filtering: Application to Seismic Multiple Removal

A year ago we talked about a technique for Adaptive multiple subtraction with wavelet-based complex unary Wiener filters. The field of application is seismic signal processing. The fast and simple design was heuristic (helping discovery, stimulating interest as a means of furthering investigation.based on experimentation), based on an appropriate combination of "a sparsifying transform" and a closed-form one-tap, sliding-window adaptive filter. To make it more pragmatic (based on observation and real-world models), an alternative approach uses proximal algorithms to incorporate sparsity priors, either on data in redundant frame transforms and in the short-support filter design. Here is the preprint: A Primal-Dual Proximal Algorithm for Sparse Template-Based Adaptive Filtering: Application to Seismic Multiple Removal and the version published by IEEE Transactions on Signal Processing.

Unveiling meaningful geophysical information from seismic data requires to deal with both random and structured ``noises''. As their amplitude may be greater than signals of interest (primaries), additional prior information is especially important in performing efficient signal separation. We address here the problem of multiple reflections, caused by  wave-field bouncing between layers. Since only approximate models of these phenomena are available, we propose a flexible framework for time-varying adaptive filtering of seismic signals, using sparse representations,  based on inaccurate templates. We recast the joint estimation of adaptive filters and primaries in a new convex variational formulation. This approach allows us to incorporate plausible knowledge about noise statistics, data sparsity and slow filter variation in parsimony-promoting wavelet frames.  The designed primal-dual algorithm solves a  constrained  minimization problem that alleviates standard regularization issues in finding hyperparameters. The approach demonstrates  significantly good performance in low signal-to-noise ratio conditions, both for simulated and real field data.

While applied here to seismic signal, the concept is heavily related to pattern matching in images, echo cancellation in audio or voice signals, exemplar search in speech.

Multirate structures, multiscale decompositions: two years after

Signal Processing

Two years ago, in December 2011, a special issue of Signal Processing was published on the theme of Advances in Multirate Filter Bank Structures and Multiscale Representations. Eleven papers, ranging from 1D or 2D data, spanning topics from filter frame design to compression, browsing applications from audio to medical imaging. This issue was very rich in interesting papers, thanks to the authors and reviewers.

Can one say a little more? Of course, bibliometrics or scientometrics generate a lot of debates. Generally, such indicators do not mean anything absolute, they may only serve as a ground for discussion. Let us just compare the figures with the journal statistics: Signal Processing has a two-year Impact Factor on 1.851 (2012). Special issue citation data is tabulated in the following array:

Citation sources (2013/12/14)	Elsevier	ISI-Thomson	Google
Title	Scopus	WoS	Scholar
A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity	13	11	20
Augmented Lagrangian based Reconstruction of non-uniformly sub-Nyquist sampled MRI data	13	7	18
Bandlet Image Estimation with Model Selection	1	0	2
Matching Pursuit Shrinkage in Hilbert Spaces	0	0	2
Non Separable Lifting Scheme with Adaptive Update Step for Still and Stereo Image Coding	3	2	7
Multivariate empirical mode decomposition and application to multichannel filtering	11	5	14
Resonance-Based Signal Decomposition: A New Sparsity-Enabled Signal Analysis Method	18	5	24
Activelets: Wavelets for Sparse Representation of Hemodynamic Responses	10	7	12
Fast orthogonal sparse approximation algorithms over local dictionaries	4	2	6
Recursive Nearest Neighbor Search in a Sparse and Multiscale Domain for Comparing Audio Signals	0	0	0
Symmetric Tight Frame Wavelets With Dilation Factor M=4	1	0	1

One observes that the citation counts for Elsevier Scopus, ISI-Thomson Web of Science or Google Scholar are very much uneven. As usual, Google Scholar lies above the two others. This observation should suffice, at least for genuine data scientists, to refrain from using carelessly a single number such as the h-index, without citing the source. When a reality (one's paper visibility) is given three very different values by three similar sensors (with different vendors), one should be cautious about using only the sensor value she-he prefers. This attitude should be very uncoherent for people claiming they can denoise measurements, restore signals, analyze images with precise tools. And forget all about the scientific method when it comes to quantified self-performance.

Then the counts are very different for the different papers. So an average index (here 3.5, or 2.8 without the overview paper) is not meaningful. One potential sound approach is to resort to range statistics, with the least favorable index (ISI-Thomson-WoS). Four papers have not been cited yet. The seven others have a citation count [11, 7, 7, 5, 5, 2, 2] greater than the impact factor (1.851). Qualitatively, the performance of this special issue may be said a little above the journal's performance.

Of course, the eleven papers have a longer life ahead than a two-year run.The only thing we may wish is an absolute improvement of their visibility and influence. Meet you in December 2015, to see how the pack has grown. Here is the paper leaflet.

Keywords: Review; Multiscale; Geometric representations; Oriented decompositions; Scale-space; Wavelets; Atoms; Sparsity; Redundancy; Bases; Frames; Edges; Textures; Image processing; Haar wavelet; Non-Euclidean wavelets; Augmented Lagrangian methods; MRI reconstruction; Non-uniform Fourier transform; Shearlet; Compressed sensing; Model selection; White noise model; Image estimation; Geometrically regular functions; Bandlets; Dictionary; Matching pursuit; Shrinkage; Sparse representation; Lossless compression; Progressive reconstruction; Lifting schemes; Separable transforms; Non-separable transforms; Adaptive transforms; Multiresolution analysis; Wavelets; Stereo coding; Mono- and multivariate empirical mode decomposition; Filter bank structure; Electroencephalography data analysis; Sparse signal representation; Constant-Q transform; Wavelet transform; Morphological component analysis; BOLD fMRI; Hemodynamic response; Wavelet design; Sparsity; l1 minimization; Sparse approximation; Greedy algorithms; Shift invariance; Orthogonal Matching Pursuit; Multiscale decomposition; Sparse approximation; Time—frequency dictionary; Audio similarity; Wavelet transform; Frame; Symmetric filterbanks; Multiresolution analysis