[Où l'on propose le néologisme
dédoménologie pour désigner la technique, la pratique, la science du traitement de signal et de l'analyse d'images, au cœur du domaine naissant de la
science des données, en passant par Euclide]
Ce sont les mots qui existent, ce qui n'a pas de nom n'existe pas. Le mot lumière existe, la lumière n'existe pas. (Francis Picabia, ou Francis-Marie Martinez de Picabia, Écrits)
Quelle analyste d'image, quel traiteur de signal n'a jamais eu des difficultés à décrire son métier ? Pas en détail bien sûr :
En fait, je m'intéresse aux propriétés cyclostationnaires des coefficients d'ondelettes de mouvements browniens fractionnaires dans les images de textures. Enfin quand je dis cyclostationnaire, il faut entendre périodiquement corrélé, hein, je ne parle pas des processus presque périodiques.
Le traitement du signal, des images ou des données
requiert très souvent des périphrases. Des exemples parlants :
Tu vois Photoshop ?
Très mauvais exemple. L'interlocuteur voit rapidement une journée de "travail" à bouger le mulot pour changer une teinte, sélectionner des objets à la baguette magique.
Tu connais le mp3 ? Le format JPEG ?
Et de rentrer dans des détails sordides de données numériques redondantes, de quantification, dont on cherche à extraire uniquement la partie perceptible utile. Avec le risque de remarques déplacées :
Le son du mp3, moi je trouver ça nul par rapport au vinyl ! [C'est pas gagné...]
L'analyste de signaux, le traiteur d'images,
mais quel bruit fait-il ? C'est souvent une histoire de bruit d'ailleurs, un signal propre, une image nette, des données obvies, personne ne nous demande jamais de les analyser, de les traiter. C'est un peu comme les médecins en occident : ils voient peu de gens en bonne santé, à part les hypocondriaques, qui ont bien sûr un petit problème de santé, à un autre niveau. Le traitement de signal, l'analyse de données, on n'en fait pas en petite classe, du moins pas directement. Ce n'est pas au baccalauréat. Donc cette matière, la plupart des gens n'ont pas eu à la subir, et ayant peu de contact avec des mesures expérimentales, rares sont ceux qui ont dû avouer qu'ils ne savaient pas traiter les échantillons chèrement acquis. Pourtant, la donnée numérique est au cœur du monde réel, et il est fort possible que cela ne fasse qu'empirer.
 |
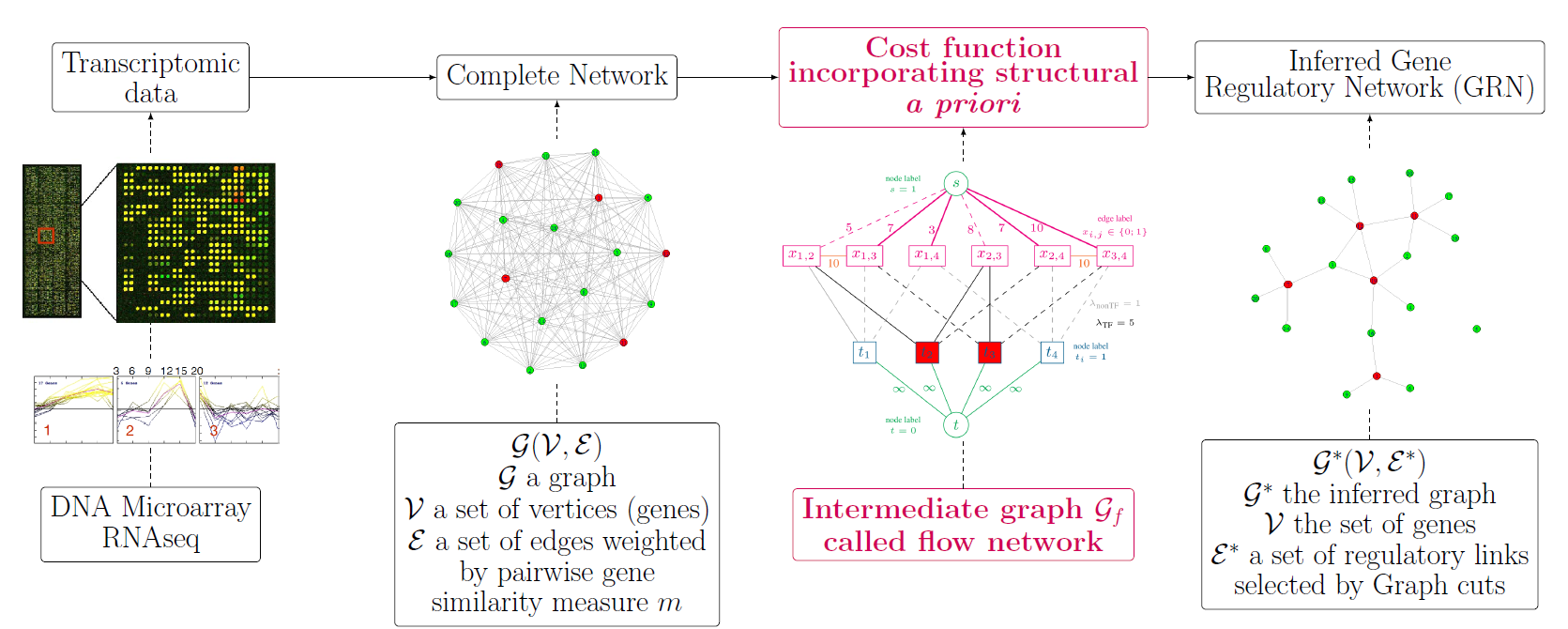
| Traitement d'images pour la science de la physique des matériaux |
Ah ça, les mathématiques, on voit bien. La physique, la biologie, c'est à peu près clair. La chimie, évident. De loin, on sent que c'est compliqué, mais que ces gens gens-là se comprennent. Il y a des cases pour cela à l'Académie des sciences. Parfois ils ont des prix Nobel. Pas en mathématiques, mais on sait bien qu'il y une espèce de prix Nobel des mathématiques, la médaille Fields. Et pourtant on connait mal le sens de ces mots :
mathématiques vient du grec par le latin, avec un sens original de "science, connaissance". Physique vient de la "connaissance de la nature". Dans biologie, il y a le vivant, les produits bios... La chimie, c'est un peu plus compliqué (des mélanges, de la magie noire, de l'arabe et du grec). Mais statistiques, on retrouve la trace de l’État : science qui a pour but de faire connaître l'étendue, la population, les ressources agricoles et industrielles d'un État. L'électronique, on voit bien les petits électrons qui bougent dans les fils.
 |
| Analyse de signal chromatographique bidimensionnel |
Et pourtant, la réalité scientifique est bien plus éparpillée : un biologiste qui étudie une bactérie a souvent peu à partager avec une spécialiste des champignons. Rien à voir, comme un spécialiste des dauphins et un lombriculteur.
Cédric Villani, qui fait un grand effort de divulgation ces derniers temps (Les mathématiques sont un art comme les autres), et qui sera invité du prochain congrès de la communauté francophone et groupement de recherche et d'études du traitement du signal et de l'image (GRETSI 2015) à Lyon, montre une prudence naturelle quand on l'interroge sur d'autres mathématiques que les siennes. Physiciens des particules et mécaniciens des fluides se rencontrent rarement. La carte des sciences est bien plus complexe que les contribuables ne le pensent généralement.
 |
| Une carte des sciences en graphe |
Comme les médecins qui ne soignent pas uniquement leurs bobos, les traiteurs de signaux traitent souvent les problèmes des autres disciplines. Les
images pour la physique des matériaux, les signaux de chromatographie pour les chimistes analytiques, les réflexions sismiques des géophysiciens. Les traiteurs de signaux, les analyseurs d'images doivent comprendre un peu de ces disciplines. Savoir utiliser différentes techniques (analyse spectrale, statistiques, algèbre linéaire, modélisation paramétrique, optimisation, normalisation) et les mettre en pratique par des algorithmes et des programmes, même du matériel.
 |
| Déconvolution aveugle de réflexions sismiques |
Il y a donc de la pratique (praxis) et de la technique (tekné) dans cette discipline composite, à la frontière d'autres sciences et disciplines. Il a fallu d'abord des mesures expérimentales avant de pouvoir les traiter. Personnellement, je me sens un praticien de certains types de données. Je connais leurs pathologies de base, j'ai quelques traitements qui marchent parfois. Technicien de la donnée, praticien de l'échantillon, ça donnerait des métiers d'infopracteurs/trices ou
infopraticiens/praticiennes, d'infotechniciens/ciennes. J’aime a priori l’idée de rendre leur noblesse aux termes de praxis et de tekné. Donc « infopraxie » ou
« infotechnie » comme nom de discipline ? Mais -technie, -praxie ça fait rebouteux, mécanicien auto. Et puis info, c’est trop « informatique ». Datalogie, ça aurait pu être bien : c'est une racine composite latino-hellénique, qui reflète bien l'aspect interdisciplinaire de cette science. Malheureusement, c'est
déjà pris par l'informatique à nouveau (computer science). Il faudrait donc un truc plus sérieux.
Et par un tournant de sérendipité, je tombe sur un texte d’
Euclide, Dedomena qui a vu son titre traduit en latin en « data ». Il s'agit d'un texte sur la nature et les implications d'information donnée pour résoudre un problème géométrique. On y est. Il définit comment un objet est décrit en forme, en position, en grandeur. Ces critères sont très nettement ceux que l'on extrait au quotidien de données numériques. Et puis Euclide, c'est un bel hommage : les espaces euclidiens sont à la base de nombreux concepts algorithmes, et la minimisation de la distance euclidienne, c'est notre pain quotidien. Il suffit de regarder cet interlude de Martin Vetterli, From Euclid to Hilbert, Digital Signal Processing.
Alors je propose de renommer le traitement de signal ou des images, des données en général, en
dédoménologie, ou l’art de ceux qui parlent de, qui analysent des données. Cela plonge directement le traitement des signaux et des images au centre de la
science des données en général. Ça aurait de la gueule sur une carte de visite, non ? Une mnémonique pour retenir ce terme : des domaines aux logis.
A partir de là, on peut étendre le vocabulaire à la
dédoménotaxie, pour les opérations de classement, de tri de données (pour coller
Euclide dans un taxi, c'est ici), à la dédoménotropie pour les flux de données, la dédoménomancie pour les aspects de prédiction (façon predictive analytics). Dénoménonomie, à la manière de l'astronomie, c'est peut-être dur à porter. Voila pour la science. Pour les aspects sociétaux, la mode est à la crainte des usages de manipulation de l'opinion et d'une gouvernance accrue par les données : dédoménodoxie et dédoménocratie. Attention donc à la dédoménophobie.
P. S. : après des recherches complémentaires, en anglais, le mot
dedomenology pour désigner le concept de data science semble déjà avoir été émis, sans trop de succès.
P. S. 2 : on me signale (Hervé T.) que l'homophonie avec démonologie est suspecte. D'un : le dialbe est dans les détails, en science des données aussi. De deux : le démon de Maxwell, sans autre la qualité d'un filtre, est le parangon du tri du bon grain et de l'ivraie. De trois : en informatique; un démon est :
Un daemon (prononcé /ˈdiːmən/ ou /ˈdeɪmən/, du grec δαιμων) ou démon désigne un type de programme informatique, un processus ou un ensemble de processus qui s'exécute en arrière-plan plutôt que sous le contrôle direct d'un utilisateur.
Tout est dit.