Sparse seismic data restoration: a PhD defense

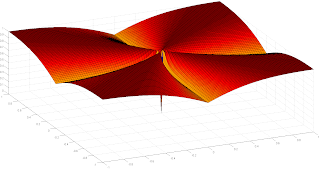
Smoothed $\ell_1/\ell_2$ function for a sparse $\ell_0$ surrogate

Mai Quyen PHAM has defended her PhD thesis on July 15th, 2015 at 10.00 am, on the topic of "Seismic wave field restoration using sparse representations and quantitative analysis” (manuscript in pdf), at Université Paris-Est, bâtiment Copernic, amphithéâtre Maurice Gross, 5 boulevard Descartes (RER A, Noisy-Champs), 77420 Champs-sur-Marne. 

Its focus is twofold:
1) sparse adaptive filtering with approximate templates in redundant and geometric wavelet frames (akin to echo cancellation in speech),

2) sparse blind deconvolution for parsimonious reflectivity signals with l1/l2 norm ratio penalty

This work has notably been published in two journal papers
*Euclid in a Taxicab: Sparse Blind Deconvolution with Smoothed l_1/l_2
Audrey Repetti, Mai Quyen-Pham, Laurent Duval, Émilie Chouzenoux, Jean-Christophe Pesquet
IEEE Signal Processing Letters, May 2015, Volume 22, Number 5, pages 539-543.
http://dx.doi.org/10.1109/LSP.2014.2362861

Matlab SOOT sparse blind deconvolution code (http://lc.cx/soot)

Abstract: The l1/l2 ratio regularization function has shown good performance for retrieving sparse signals in a number of recent works, in the context of blind deconvolution. Indeed, it benefits from a scale invariance property much desirable in the blind context. However, the l1/l2 function raises some difficulties when solving the nonconvex and nonsmooth minimization problems resulting from the use of such a penalty term in current restoration methods. In this paper, we propose a new penalty based on a smooth approximation to the l1/l2 function. In addition, we develop a proximal-based algorithm to solve variational problems involving this function and we derive theoretical convergence results. We demonstrate the effectiveness of our method through a comparison with a recent alternating optimization strategy dealing with the exact l1/l2 term, on an application to seismic data blind deconvolution.

*A Primal-Dual Proximal Algorithm for Sparse Template-Based Adaptive Filtering: Application to Seismic Multiple Removal
Mai-Quyen Pham, Laurent Duval, Caroline Chaux, Jean-Christophe Pesquet
IEEE Transactions on Signal Processing, August 2014, Volume 62, Issue 16, pages 4256-4269
http://dx.doi.org/10.1109/TSP.2014.2331614

PhD Committee:
Reporter Jean-Francois Aujol Prof. Université de Bordeaux
Reporter Mauricio D Sacchi Prof. University of Alberta
Examiner Jérôme Mars Prof. Grenoble-INP
Examiner Mai K. Nguyen Prof. Université de Cergy-Pontoise
PhD supervisor Jean-Christophe Pesquet Prof. Université Paris-Est Marne-la-Vallée
PhD co-supervisor Laurent Duval Dr. IFP Energies nouvelles (IFPEN)
PhD co-supervisor Caroline Chaux CNRS researcher, I2M, Aix-Marseille Université

Map to Copernic building

Abstract: This thesis deals with two different problems within the framework of convex and non convex optimization. The first one is an application to multiple removal in seismic data with adaptive filters and the second one is an application to blind deconvolution problem that produces characteristics closest to the Earth layers. More precisely: Unveiling meaningful geophysical information from seismic data requires to deal with both random and structured “noises”. As their amplitude may be greater than signals of interest (primaries), additional prior information is especially important in performing efficient signal separation. We address here the problem of multiple reflections, caused by wave-field bouncing between layers. Since only approximate models of these phenomena are available, we propose a flexible framework for time-varying adaptive filtering of seismic signals, using sparse representations, based on inaccurate templates. We recast the joint estimation of adaptive filters and primaries in a new convex variational formulation. This approach allows us to incorporate plausible knowledge about noise statistics, data sparsity and slow filter variation in parsimony-promoting wavelet transforms. The designed primal-dual algorithm solves a constrained minimization problem that alleviates standard regularization issues in finding hyperparameters. The approach demonstrates significantly good performance in low signal-to-noise ratio conditions, both for simulated and real field seismic data. In seismic exploration, a seismic signal (e.g. primary signal) is often represented as the results of a convolution between the “seismic wavelet” and the reflectivity series. The second goal of this thesis is to deconvolve them from the seismic signal which is presented in Chapter 6. The main idea of this work is to use an additional premise that the reflections occur as sparsely restricted, for which a study on the “sparsity measure” is considered. Some well known methods that fall in this category are proposed such as (Sacchi et al., 1994; Sacchi, 1997). We propose a new penalty based on a smooth approximation of the ℓ1/ℓ2 function that makes a difficult nonconvex minimization problem. We develop a proximal-based algorithm to solve variational problems involving this function and we derive theoretical convergence results. We demonstrate the effectiveness of our method through a comparison with a recent alternating optimization strategy dealing with the exact ℓ1/ℓ2 term.