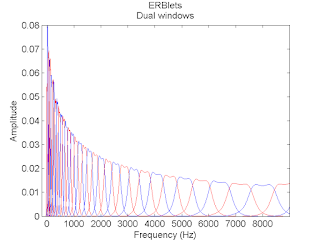
ERBlet transform (on WITS: Where is the starlet)

ERBlet transform dual frame spectrum

After about a hundred starlets or wavelets in *let, the newborn ERBlet borrows from the auditory scale, namely the Equivalent Rectangular Bandwidth and the non-stationary Gabor transforms (NSGT). See more at WITS: where is the Starlet. The attendant Matlab toolbox is there (ICASSP 2013).

ERBlet

In short:	A linear and invertible time-frequency transformation adapted to human auditory perception, for masking and perceptual sparsity
Etymology:	From the ERB scale or Equivalent Rectangular Bandwidth

filter banks, devised for auditory based-representation, following the philosophy of third-octave filter banks. See also Frequency Analysis and Masking - MIT, Brian C. J. Moore, 1995 and Bark and ERB Bilinear Transforms - Stanford University, by J. O. Smith III
Origin:
Thibaud Necciari, Design and implementation of the ERBlet transform, FLAME 12 (Frames and Linear Operators for Acoustical Modeling and Parameter Estimation), 2012

Time-frequency representations are widely used in audio applications involving sound analysis-synthesis. For such applications, obtaining a time-frequency transform that accounts for some aspects of human auditory perception is of high interest. To that end, we exploit the theory of non-stationary Gabor frames to obtain a perception-based, linear, and perfectly invertible time-frequency transform. Our goal is to design a non-stationary Gabor transform (NSGT) whose time-frequency resolution best matches the time-frequency analysis properties by the ear. The peripheral auditory system can be modeled in a first approximation as a bank of bandpass filters whose bandwidth increases with increasing center frequency. These so-called “auditory filters” are characterized by their equivalent rectangular bandwidths (ERB) that follow the ERB scale. Here, we use a NSGT with resolution evolving across frequency to mimic the ERB scale, thereby naming the resulting paradigm "ERBlet transform". Preliminary results will be presented. Following discussion shall focus on finding the "best" transform settings allowing to achieve perfect reconstruction while minimizing redundancy.

Thibaud Necciari with P. Balazs, B. Laback, P. Soendergaard, R. Kronland-Martinet, S. Meunier, S. Savel, and S. Ystad, The ERBlet transform, auditory time-frequency masking and perceptual sparsity, 2nd SPLab Workshop, October 24–26, 2012, Brno

The ERBlet transform, time-frequency masking and perceptual sparsity Time-frequency (TF) representations are widely used in audio applications involving sound analysis-synthesis. For such applications, obtaining an invertible TF transform that accounts for some aspects of human auditory perception is of high interest. To that end, we combine results of non-stationary signal processing and psychoacoustics. First, we exploit the theory of non-stationary Gabor frames to obtain a linear and perfectly invertible non-stationary Gabor transform (NSGT) whose TF resolution best matches the TF analysis properties by the ear. The peripheral auditory system can be modeled in a first approximation as a bank of bandpass filters whose bandwidth increases with increasing center frequency. These so-called “auditory filters” are characterized by their equivalent rectangular bandwidths (ERB) that follow the ERB scale. Here, we use a NSGT with resolution evolving across frequency to mimic the ERB scale, thereby naming the resulting paradigm “ERBlet transform”. Second, we exploit recent psychoacoustical data on auditory TF masking to find an approximation of the ERBlet that keeps only the audible components (perceptual sparsity criterion). Our long-term goal is to obtain a perceptually relevant signal representation, i.e., as close as possible to “what we see is what we hear”. Auditory masking occurs when the detection of a sound (referred to as the “target” in psychoacoustics) is degraded by the presence of another sound (the “masker”). To accurately predict auditory masking in the TF plane, TF masking data for masker and target signals with a good localization in the TF plane are required. To our knowledge, these data are not available in the literature. Therefore, we conducted psychoacoustical experiments to obtain a measure of the TF spread of masking produced by a Gaussian TF atom. The ERBlet transform and the psychoacoustical data on TF masking will be presented. The implementation of the perceptual sparsity criterion in the ERBlet will be discussed.

Contributors:
Thibaud Necciari with P. Balazs, B. Laback, P. Soendergaard, R. Kronland-Martinet, S. Meunier, S. Savel, and S. Ystad
Some properties:
Develops a non-stationary Gabor transform (NSGT) [Theory, Implementation and Application of Nonstationary Gabor Frames, P. Balazs et al., J. Comput. Appl. Math., 2011] with resolution evolving over frequency to mimic the ERB scale (Equivalent Rectangular Bandwidth, after B. C. J. Moore and B. R. Glasberg, "Suggested formulae for calculating auditory-filter bandwidths and excitation patterns", J. Acoustical Society of America 74:750-753, 1983). Linear and invertible time-frequency transform adapted to human auditory perception.
Anecdote:A Matlab implementation of the ERBlet transform should appear in 2013 for ICASSP in Vancouver.

Group-pride: IFPEN Ranking

So, i know, it is just another ranking. Well...

Press releases : IFP Energies nouvelles makes Thomson Reuters' Top 100 Global Innovators in 2012

05 December 2012

IFP Energies nouvelles (IFPEN) has earned a place in Thomson Reuters' list of Top 100 Global Innovators for the second year running.

The ranking, which measures innovation in intellectual property, is determined using a variety of patent-related criteria. This includes application success (the ratio of published applications to granted patents), the volume of patents in innovative areas like new technologies, global coverage (inventions patented with all "quadrilateral" patent authorities, i.e. in Europe, Japan, China and the US) and the patents' impact (the number of times they are cited by competitors).

The award is due recognition of IFPEN's policy of innovation and industrial development, aimed at protecting research, promoting technology transfer to industry, and creating wealth and jobs.

It is not the first time IFPEN has been rewarded for innovation. In 2011 the French institute for intellectual property (INPI) ranked it 11th in France by number of published patents. That puts IFPEN among the top three research bodies in France, with the French Atomic Energy Commission (CEA), and the French National Scientific Research Center (CNRS). When adjusted to account for workforce (1,700 staff), IFPEN climbs to number one.

Devo, I Can't Get No Satisfaction (Cover)

Beaujolais nouveau: anagrams and Cambridge University research

According to a researcher (hic) at Salonic  University, it doesn't matter in what order the letters in a word are, the only important thing is the quantity of Beaujolais Nouveau wine you have drunk before. This external advertising panel outside a Nicolas shop distills: "Le Beaujolais nouveau est arrivé" in a drunkard anagram: "Le beuajolias nuovaeu est avriré". See what it does to the poor Alan Parsons Project.

The ad takes on the September 2003 hoax on the unimportance of the order of letters, according to a forged  researcher (sic) at Cambridge University (Aoccdrnig to a rscheearch at Cmabrigde Uinervtisy).

Even if not completely invalid, the hoax may be checked with Switcharoo! (Order of letters in a word doesn't matter? The hell it ...). For instance, it kinda works on Wim Sweldens' definition of the wavelet in the introduction for his PhD thesis, Construction and Application of Wavelets in Numerical Analysis, in 1994 (see the scrambled WITS: Where is the Starlet?)

Original: Uit de wiskundige analyse volgde dat de integraal van deze functie nul moet zijn en dat deze functie naar nul moet convergeren als het argument naar oneindig gaat. M.a.w. deze functie moet een beetje "schommelen" en dan geleidelijk uitsterven; het is een soort "lokaal golfje".

Scrambled: Uit de wskngdiuie aaslyne vdogle dat de igtanaerl van deze ficntue nul meot zijn en dat deze ficntue naar nul meot ceervongern als het agnumert naar oineindg gaat. M.a.w. deze ficntue meot een bteeje "seoemmhcln" en dan gileeeiljdk uirsteevtn; het is een sroot "lakaol gfojle".

It works with Dutch. I cannot equally read both texts. Here are two interesting texts, with studies in different languages, pertaining to the case. None from Cambridge university.

Carol Whitney. How the brain encodes the order of letters in a printed word: the SERIOL model and selective literature review. Psychon Bull Rev. 2001 Jun. 8(2):221-43, and associated publications.

This paper describes a novel theoretical framework of how the position of a letter within a string is encoded, the SERIOL model (sequential encoding regulated by inputs to oscillations within letter units). Letter order is represented by a temporal activation pattern across letter units, as is consistent with current theories of information coding based on the precise timing of neural spikes. The framework specifies how this pattern is invoked via an activation gradient that interacts with subthreshold oscillations and how it is decoded via contextual units that activate word units. Using mathematical modeling, this theoretical framework is shown to account for the experimental data from a wide variety of string-processing studies, including hemispheric asymmetries, the optimal viewing position, and positional priming effects.

Jonathan Grainger and Thomas Hannagan. Explaining word recognition, reading, the universe, and beyond: A modest proposal. Behavioral and Brain Sciences, August 2012.

In the last decade, reading research has seen a paradigmatic shift. A new wave of computational models of orthographic processing  that  offer  various  forms  of  noisy  position  or  context-sensitive  coding  have  revolutionized  the  field  of  visual  word recognition. The influx of such models stems mainly from consistent ?ndings, coming mostly from European languages, regarding an apparent insensitivity of skilled readers to letter order. Underlying the current revolution is the theoretical assumption that the insensitivity of readers to letter order reflects the special way in which the human brain encodes the position of letters in printed words. The present article discusses the theoretical shortcomings and misconceptions of this approach to visual word recognition. A systematic  review  of  data  obtained  from  a  variety  of  languages  demonstrates  that  letter-order  insensitivity  is  neither  a  general property of the cognitive system nor a property of the brain in encoding letters. Rather, it is a variant and idiosyncratic characteristic of some languages, mostly European, reflecting a strategy of optimizing encoding resources, given the specific structure of words. Since the main goal of reading research is to develop theories that describe the fundamental and invariant phenomena of reading across orthographies, an alternative approach to model visual word recognition is offered. The dimensions of a possible universal model of reading, which outlines the common cognitive operations involved in orthographic processing in all writing systems, are discussed.

Do not "Drunk in the gutter", "Greet unkind truth".

ICASSP 2013: Special sessions

ICASSP 2013 (to to held in Vancouver, Canada, May 2013) deadline has been nicely extended to November 30th, 2012. (Rare) updates on Twitter. From the grapevine, the accepted special session list includes the following:

Organizers: Mark Plumbley, Dimitris Giannoulis, Mathieu Lagrange

• Title: Acoustic Event Detection and Scene Analysis.

Organizers: Mauro Barni, Fernando Pérez-González

• Title: Advances in adversary-aware signal processing.

Organizers: Tao Zhang and Philip Loizou

• Title: Challenges, Solutions and Future Directions in Signal Processing Research for Hearing Instruments.

Organizers: Ali N. Akansu and Ilya Pollak

• Title: Financial Signal Processing and Electronic Trading.

Organizers: Li Deng, Geoff Hinton, Brian Kingsbury

• Title: New types of deep neural network learning for speech recognition and related applications.

Organizers: Laurent Duval, Leonardo T. Duarte, Christian Jutten

• Title: Signal Processing for Chemical Sensing.

Organizers: Yuzhe Jin, Kuansan Wang

• Title: Sparse Signal Techniques for Web Information Processing.

Organizers: Jay Unnikrishnan, Martin Vetterli, Richard Baraniuk 

• Title: Signal Processing Education in the Internet Age.

SEG 2012: From Las Vegas with notes

Back in 2002 ICASSP, i thought Orlando had a little something... artificial. Fake trees, weird hotels. Ten years later in 2012 SEG (Society of Explorations Geophysicists) annual meeting in Las Vegas, well the fake fragrance mixes even more with air conditioned, and the weather is really cool. No need to keep twitting on the event because Matt Hall at Agile* does it already. The papers i'll have to study a little deeper are the following:

• Bandwidth enhancement by inverse-Q filtering or time-varying Wiener deconvolution? (Mirko van der Baan), getting the best out of the two techniques.
• Decon in the log domain with variable gain (Jon Claerbout, Qiang Fu, and Antoine Guitton), revisiting Ricker and Wiener in white/black/white
• Gabor deconvolution using regularized smoothing (Zengbao Chen et al.), adding regularization on Margrave decon.
• Guided seismic-to-well tying based on dynamic time warping (Roberto Henry Herrera and Mirko van der Baan)

I'm keeping a last word for Generalized windowed transforms for seismic processing and imaging (Charles C. Mosher). Having worked with wavelets in geophysics for decades, Chuck comes up with a 20 years' work on developing a slighly redundant windowed transform, based on finite support filters in the frequency domain associated with fractional subsampling, to reduce the aliasing, and moving artifacts to some form of blending. This ends up in a non tight frame, mostly implemented in the Fourier transformed domain. 

This transform is meant to be used in blended acquistion, or even compressing sensing, two of the current trends in geophysical meetings. No wonder, the cost of data acquisition is so high in seismic exploration that one may expect huge savings if they succeed in reducing the acquisition rate by just a factor of two. What puzzles me, still, is that the same petroleum industry which could not loose 1-bit out of 24-integer or 32-bit float data in lossy compression, now looked at blended acquisition (followed by source separation) or compressive sensing has potential data deluge saviors. I even have the feeling that a few people cannot yet tell the difference between those two.

Who compressively senses compressive sensors?

Who compressively senses the compressive sensing folks (cf. Quis custodiet ipsos custodes?)? In an exchange among technical chairs for a conference with a close deadline, we notice the following mention:

Please pay particular attention to reviewers who can deal with compressed sensing papers. Extrapolating from previous years, there are typically almost a 100 papers in compressed sensing - and so we need a lot of capable reviewers in the area.

Impressive. So who does compressively sense the compressive sensing community? Nuit Blanche does sense it, maybe not quite compressively (hence, its audience). I guess there exists redundancy in the published stuff, should one try to reduce drastically the selection on compressive sensing, not based on "peer evaluation", maybe on random picking? Or assuming some Finite Rate of Innovation in a period of time? Hurry up, rumors are the NSF (not NFS nor NHS, thank you Igor) may shrink the funding on such topics...


All along the watch tower (Bob Dylan) by Calvin Russell

Adaptive seismic multiple removal with complex wavelet (paper)

The November-December 2012 issue of Geophysics (Volume 77, Issue 6) features (at last) a recent work performed on model-based, adaptive multiple removal in seismic. The concept is illustrated on the figure to the left. Signal obtained from direct reflections of interest (blue) are mixing with other waves bouncing between layers (red). They look alike except for differential attenuation in the frequency domains, different slopes in CMP gathers. Those interested could have a look at the booklet Seismic multiple removal techniques: past, present and future by Eric J. (Dirk) Verschuur. Those more patient may want to waiting for Seismic Multiple Elimination Techniques, by the same author, which should be published in June 2013.As the problem is quite complex per se, hundred of papers have been devoted to multiple elimination techniques, since the January 1948 special issue of Geophysics. A common approach consists in first computing one or several approximate models of the multiple reflections, and then trying to adaptively substract the model from the data. Such techniques usually combine an adapted representation (Fourier, Radon, different breeds of wavelets) and a matching or separation technique. The one we finally published resides at one end of the representation/matching spectrum, to cope with the industrial partner requirements. A somewhat redundant complex wavelet tranform (and yes, combining a Morlet wavelet frame and the complex trace, so to say) and a very simple sliding window 1-tap adaptive filter estimation on the complex scalogram, to adapt and remove a template disturbance signal from the original seismic trace. Maybe not the most theoretically proven approach, but a decent, fancy blend of complex wavelets and adaptive filtering, and some industrialized code that works. And a milestone in a nice collaborative venture, especially with Sergi Ventosa, now at IPGP. And finally published (took 1.5 years). So here it is:

Adaptive multiple subtraction with wavelet-based complex unary Wiener filters (arxiv, doi, page), Geophysics, 2012, November-December

Sergi Ventosa, Sylvain Le Roy, Irène Huard, Antonio Pica, Hérald Rabeson, Patrice Ricarte, Laurent Duval

Abstract: Adaptive subtraction is a key element in predictive multiple-suppression methods. It minimizes misalignments and amplitude differences between modeled and actual multiples , and thus reduces multiple contamination in the dataset after subtraction. The challenge consists in attenuating multiples without distorting primaries, despite the high cross-correlation between their waveform. For this purpose, this complicated wide-band problem is decomposed into a set of more tractable narrow-band problems using a 1D complex wavelet frame. This decomposition enables a single-pass adaptive subtraction via single-sample (unary) complex Wiener filters, consistently estimated on overlapping windows in a complex wavelet transformed domain. Each unary filter compensates amplitude differences within its frequency support, and rectifies more robustly small and large misalignment errors through phase and integer delay corrections . This approach greatly simplifies the matching filter estimation and, despite its simplicity, compares promisingly with standard adaptive 2D methods, on both synthetic and field data.

The preprint version is available, with nice color figures, under the umbrella of Arxiv. Next in line: explore other ends of the matching/transform spectrum. Comments welcome.

What is a color?

Typically the kind of image that makes me (still) love image processing. So the "light green" spiraled stripelets have the same absolute color coordinates (yes, R,G,B) as the "light blue" ones. I have checked it with XnView.

There is still room for image processing algorithms that meet vision stimuli.

The two-penny philosophical question: do these two colors actually merge at the aliased warped end in the center? Indeed, the phenomenon is related to the scale of observation, as one may obseve by zooming in and see how the green and the blue reduce their perceptual distance. Funnily enough, the illusion also works with at least one color blind and image processing specialist colleague (Frédéric Morain-Nicolier @ Pixel Shaker) who has been kind enough to discuss these issues. So below is the thumbnail and its enlarged version. Of course, you cannot fully trust the present image renderer,. Try by yourself.

Akiyoshi Illusion page:
http://www.ritsumei.ac.jp/~akitaoka/index-e.html

SIVA Conferences : concern fees (update)

Although conferences = concern fees (with the anagram equivalence) for a few organizers, they allow to grab a few call for papers to other conferences. Grabbed from EUSIPCO 2012, along with cfp1 and cfp2 (on time-frequency theory and applications), and after a couple of proofs from a finally painfully published paper in Geophysics, the recent opening of GRETSI 2013 website in Brest, France, provides a good opportunity to release the latest updates on Signal, Image and Volume Analysis (SIVA) Conferences:

Eurographics 2013 (Annual conference of the European Association for Computer Graphics) calls for papers on 21/09/2013. CVPR 2015 (IEEE Conference on Computer Vision and Pattern Recognition) is announced in Boston, Massachussetts, USA; ICIP 2016 (IEEE International Conference on Image Processing) in Phoenix, Arizona, USA; ICCV 2015 (International Conference on Computer Vision) in Santiago, Chile. 

One of the next target is ICASSP 2013 in Vancouver, Canada, with submission deadline on 19/11/2012. And many more at SIVA Conferences...

For those interested in writing time-frequency papers, two special issue call for papers:

• Call for Papers (CfP): Special issue on time-frequency methods for condition based maintenance and modal analysis
• Special issue on Signal Processing Magazine: Time-frequency analysis and applications

Time-frequency methods for condition based maintenance: call for papers

Call for Papers (CfP): Special issue on time-frequency methods for condition based maintenance and modal analysis

In recent years, research in the area of Condition-Based Maintenance (CBM) and Modal Analysis (MA) has been growing rapidly benefiting from the development of more advanced and accurate time-frequency methods. CBM is a decision making strategy which was introduced to recommend maintenance actions when the output of the sensors placed on the physical equipment fulfill a set of predefined criteria defining abnormal behaviors. CBM is based on using real-time data to prioritize and to optimize maintenance resources. It enables real-time diagnosis of impending failures and prognosis of remaining useful life of equipment without interrupting normal operations through analyzing and interpreting the measured data. Intensively used in CBM, the MA is concerned with the identification of the natural mode shapes and frequencies of structures or fluids under vibrational excitation.
Multi-purpose time-frequency methods like the short-time Fourier transform, the Wigner-Ville distribution or wavelets etc. are signal processing techniques which are applied in mechanical structures analysis for investigating functional parameters that are evolving in time like structural damages, cracks or deformations. Their usefulness in practice consists mainly in the fact that they are non-invasive techniques. This call for papers is aiming to stimulate not only new insides on the standard time-frequency techniques for signal processing but also recently developed methods like non-stationary Gabor frames, curvelets, adaptive wavelet families, sparse decompositions etc. with potential applications to dynamic data processing in manufacturing, mechanical structures and acoustics. Therefore, the main objective of this special issue is to bring the ideas of worldwide research community to present the latest developments and to advance the fields of CBM and MA through applications of the modern time-frequency processing techniques.

The following topics are of main interest:

• Time-frequency methods for diagnostics, prognostics and features extraction
• Time-frequency methods for modal analysis
• Wavelet-based vibration monitoring and control
• Natural frequencies identification
• Sparse signal analysis
• Online, segment-wise and parallel time-frequency implementations
• Assessment studies of different signal processing techniques
• Hardware and application constraints when building CBM systems
• Applications in radar, mechanics, acoustics, etc.

The specified topics should be viewed as guidelines but any original interpretation of the signal processing methods for CBM and MA will be considered.

Important dates:

• Manuscript due: November 30, 2012
• First Round of Reviews: January 31, 2013
• Second Round of Reviews: March 31, 2013
• Publication date: June 1, 2013

Submission Guidelines:
Authors are invited to submit their papers via the Elsevier submission web site at http://ees.elsevier.com/sigpro/login.asp and please select the Item: “Time-frequency for CBM&MA” after you log in as an author. Please also refer to the complete Author Guidelines.

Guest editors:

• Dr. Darian M. Onchis - University of Vienna & University of Resita, (darian.onchis@univie.ac.at)
• Dr. Ruqiang Yan - Southeast University, (ruqiang@seu.edu.cn)
• Dr. Pavel Rajmic - University of Brno, (rajmic@feec.vutbr.cz)

And of course remember this other recent special issue on the topic of multirate/multiscale methods in signal and image processing. Signal Processing: Special issue on Advances in Multirate Filter Bank Structures and Multiscale Representations, Vol. 91, Issue 12, Dec. 2011 (more here).

Time-frequency analysis and applications: call for papers

[Update 20120925] Special issue call for papers officialy released (deadline extended to 08/10/2012): Special issue on Time-frequency analysis and applications

The 4-page white paper should address: the motivations, importance, timeliness of the topics, an outline of the paper structure and content, some words about the authors (for the special issue editors). No style imposed: 4-page one-column would be enough.

Fresh from Eusipco 2012, a call for papers (cfp) is issued by the signal processing society, for IEEE Signal Processing Magazine:  Special issue on Time-frequency analysis and applications

The special issue (not yet on the special issue page) seeks to present recent advances in time-frequency (TF) signal analysis, using both linear and nonlinear decompositions.

Topics include:

• advances in detection, estimation and classification using TF signatures
• instantaneous frequency estimation
• robust TF signal representations
• new advances in TF localization and uncertainty principles
• multidimensional extensions of TF concepts (instantaneous frequency, coherence, Riesz transform, etc.)
• multi-sensor TF analysis and signal representations
• TF domain processing, time-varying systems, Gabor multipliers, non diagonal denoising
• data-driven methods e. g. Empirical mode decomposition (EMD), Hilbert-Huang transform and related techniques
• reassignment, synchrosqueezing and phase-based methods.

Guest editors:

• Patrick Flandrin
• Moeness Amin
• Steve McLaughlin
• Bruno Torrésani

Important dates:

• October 8, 2012 (2012/10/01): White paper (4 pages)
• October 15, 2012 (2012/10/15): Invitation notification
• January 15, 2013 (2013/01/15): Manuscript due
• March 1, 2013 (2013/03/15):  Acceptance notification
• April 15, 2013 (2013/04/15): Revised manuscript due
• June 15, 2013 (2013/06/15):  Final manuscript due
• November 2013 (2013/11/00): Publication date

Submissions here. Remember this other recent special issue on the topic of multirate/multiscale methods in signal and image processing. Signal Processing: Special issue on Advances in Multirate Filter Bank Structures and Multiscale Representations, Vol. 91, Issue 12, Dec. 2011 (more here).

Other sources: 
IEEE Signal Processing society: http://www.signalprocessingsociety.org/uploads/special_issues_deadlines/time_frequency.pdf

http://www.cmi.univ-mrs.fr/~torresan/pages/events.htm
http://www.signalprocessingsociety.org/uploads/email/SPM_time_frequency.html 

Noble praise

[Update 2014/07/15]

"Divide ut compresse" (to divide to compress) is the new motto for the coming Daubechies barony.

Ingrid Daubechies (wiki page) has just been granted? awarded? made a baroness title by the King of Belgium. She is has a PhD in Physics from Vrije Universiteit Brussel (VUB), teaches at Princeton and Duke universities, and is the present president of the "International Mathematical Union". She is famous to waveleters for many progresses, among others, in frame sampling, wavelet design (e.g. daublets & coiflets), (two-scale) difference equations, orthogonal and biorthogonal bases design, fast, integer, lifting, irregular and signal edge-aware implementation, time-frequency reassignment, inverse problems, fractal properties, compression, with a recent brush(let)strocke towards artist (van Gogh) identification, to mention a few. Have a look... Soon, she will be another distinguished line on http://fr.wikipedia.org/wiki/Cat%C3%A9gorie:Baron_belge.

• Qui sont nos nouveaux nobles?
• http://www.lalibre.be/actu/belgique/article/750104/qui-sont-nos-nouveaux-nobles.html
• Arise, Baronne Daubechies
• http://aperiodical.com/2012/07/arise-baronne-daubechie/

To start with, why not  "Where do wavelets come from?--A personal point of view", in Proc. IEEE, Special Issue on Wavelets, 84 (4), pp. 510-513, 1996?

Ternary, trinary or trit logic: of bricks and trytes (and bytes and bits)

http://www.mortati.com/glusker/fowler/
    The ternary calculating machine of Thomas Fowler

[In a word: e (2.71828...) would be the most efficient base for storing digital information. Not two, i.e. the bits. Storing on three-unit devices (trits) would be the best practical information base. Ternary arithmetic rulez]

This short post is inspired by Igor Carron's The 2-bit Aggie weather station. Igor proposes us the three-valued (bbl) system for assessing weather conditions, with a brick put outside: brown, bright, left:

• If brick is dark brown, it's a sure sign that it's raining outside. 
• If the brick is bright, then it's sunny outside. 
• If the brick is not there anymore, it's a tornado.

The weird ternary calculing machine machine on the right is not a brick (althhough the color is similar), and is better described in The ternary calculating machine of Thomas Fowler, IEEE Annals of the History of Computing, 2005, by Glusker, Hogan, and Vass.

Bender: Ahhh, what an awful dream. Ones and zeroes everywhere... and I thought I saw a two.
Fry: Don't worry, Bender: there's no such thing ...
Futurama

Among the very few scientific results i can grasp, a very few simple ones jump to my mind and keep me amazed:

• the fact that the Wiles-Fermat theorem is almost trivial in polynomial ring (see Mason-Stothers ABC theorem, based on Wronskians  for complex coefficients, showing that max(deg(A(a),deg(B(x),deg(C(x))) + 1 <= # roots (A(x)B(x)C(x))
• Cantor's diagonal argument
• statistical Stein's lemma and paradox, and some of it's signal processing applications (pdf)
• the most beautiful Euler god-existing formula, involving constants pi, e, i, 1 and 0 (from utmost to least translucency): e(i*pi)+1=0:

• van der Corput Lemma for oscillatory integrals
• Pick's theorem relating inside, border points and area in lattice polygons
• and, of course, a pair of others

The most radical one, pertaining to signal acquisition and representation, lies between the binary and the ternary systems: from bits to trits, from bytes to trytes. It states that the "most efficient" storing system is "e", from Euler's number, not to confuse with Mascheroni-Euler constant, gamma, (the one from the natural logarithm). I am quite surprised the binary system pervades so  much the present digital world that this "fact" is quite often ignored. Indeed, when i try to gather some information on that topic, i generally do not remember where to start from. Which keywords (trit for "ternary digits" similar to bits for "binary digits", or "tryte" versus "byte" for the "words" themselves, trinary or ternary), what sources?

The basic idea is that, when trying to represent a number in concise or sparse form on d-digits (or number byte-width), one could choose the biggest b-base (or bit-depth, the number of symbols per "digit") for representation. In a similar way for signal or image processing, the sparsest base or frame for a specific signal or image has this signal or image data as a vector. The simplest idea comes from minimizing the product width x depth, or e(d,b) = db, considered as a loss function.Let us compute it for all numbers from 0 to decimal N = 999999, in different numeral systems?

• Decimal: b = 10, d = 6 = ceil(log(N+1)/log(b)), db = 60,
• Binary: b = 2, d = 20, db = 40,
• Ternary: b = 3, d = 13,  db = 39,
• Quaternary: b = 4, d = 10,  db = 40.

Here we have a very local minimum at b = 3. More generaly, the objective minimizes the loss function e(b) = b/log(b) (at WolframAlpha). The non-negative real minimum is "e". The two potential contenders for practical arithmetics, or even physics, are the 2 (binary) or the 3 (ternary), the two closest integers. It is easy to note that e(2) = 2.885... while e(3) = 2.731... and e(4) = 5.771 (compare to 2.718...). This confirms the preceding decimal/binary/ternary/quaternary local minimum at 3, 2 becoming second, the ternary numeral system, is closer to the absolute minimum. So we need to add 2 and 3 and propose a "Generalized"-) Euler formula:

and, more interesting, 3 should be more compact, even for three-valued logic in computer systems. The chapter Ternary computers: the setun and the setun 70, by N. P. Brusentov and J. R. Alvarez from Moscow state university (at Google books), indicates that this is an old story:

"It is known that the ternary arithmetic has essential advantages as compared with the binary one that is used in present-day computers. In connection with this Donald Knuth assumed that the replacement of "flip-flop" for "flip-flap-flop" one a "good" day will nevertheless happen [1]. Now, when the binary computers predominate, it is hard to believe in a reality of such assumption, but if it would happen not only the computer arithmetic, but the informatics on the whole would become most simple and most perfect. The third value (Aristotle named it snmbebhkoV – attendant) what is very actual but hidden in binary logic, will become obvious and direct manipulated. Ternary logic has better accordance with the Nature and human informal thinking [2]. Unfortunately, the modern researches of the multivalued (non-binary) logic are formal and are not associated with practical requests.A remarkable exclusion is the experience of creating the ternary computers "Setun" and "Setun 70" at Moscow State University [3,4,5,6]. This experience convincingly confirms practical preferences of ternary digital technique.

The design of small digital machine "Setun" (Setun is the little river which flows into the river "Moscow" near the University) was initiated by member of the academy of Sciences S. L. Sobolev at 1956. It was assumed to create small, inexpensive computer, simple in use and service for schools, research laboratories, design offices and for manufacture control. For such goal at the computer center of the University there was formed a group of young men (4 MS and 5 BA). The joint seminar for engineers and programmers was organized and S. L. Sobolev, K. A. Semendjev, M. R. Shura-Bura, I. S. Berezin were its permanent participants. The problems of optimization of computer architecture and technical realization were examined and the variants of future computer were discussed."

I especially like the flip-flap-flop mnemonic. "Perhaps the prettiest number system of all," writes Donald E. Knuth in The Art of Computer Programming, "is the balanced ternary notation."This reminds of the first derivatives of position. Velocity and acceleration are well known, jerk is the 3rd derivative. Jounce is sometimes given for the fourth derivative. Jounce is the rate of change of jerk, over the time. But some call the 4th, 5th and 6th derivatives "Snap, "Crackle" and "Pop" (as for the Rice Crispies, as for those interested in wavelets).


This story is summarized in Third Base at American Scientist, by Brian Hayes: (printer-friendly version, 2001).

"When base 2 is too small and base 10 is too big, base 3 is just right. "

It even recalls the following conjecture:
More than 20 years ago, Paul Erdös and Ronald L. Graham published a conjecture about the ternary representation of powers of 2. They observed that 2^2 and 2^8 can be written in ternary without any 2s (the ternary numerals are 11 and 100111 respectively). But every other positive power of 2 seems to have at least one 2 in its ternary expansion; in other words, no other power of 2 is a simple sum of powers of 3. Ilan Vardi of the Institut des hautes études scientifiques has searched up to 2^6973568802 without finding a counterexample, but the conjecture remains open.

Yet, even-though the first attempts have met difficulties (check out the early 1950 High Speed Computing Devices in djvu), people are still working towards ternary physical systems: Klein M., Mol J. A., Verduijn J., Levine R. D., et al. Ternary logic implemented on a single dopant atom field effect silicon transistor. APPLIED PHYSICS LETTERS. 2010; 96(4) (see Raphael Levine).



So yes Igor, this brick-like technology does (almost) exist. Or probably in a near future. Maybe it is not practical enough yet, or the world is not ready for that. A while ago (30 years), i learned how to count in binary with my fingers (thanks to a mormon American, Chris F., thinking of you), and we have three phalanges, so i can easily switch. But the ternary politic system still does not yet exist in France.

Additional links on ternary arithmetics and trits (trytes or trybbles):

The Ternary Manifesto: Douglas W. Jones proposes (quite interesting) "An alternative basis for development of a completely incompatible digital infrastructure is presented here. This minimizes the potential for leakage of information, particularly malware and other covert content from our existing digital infrastructure. This effort can be described as taking security through obscurity as a fundamental design principle."

Unsigned and Balanced Ternary Representations by Douglas W. Jones again.On bytes and nybbles, Trytes and trybbles, the tennary equivalent of nybbles (packet of trytes)

Third Base (American Scientist): Cheaper by the Threesome 

Plagiarism: everything but the title

Cannot remember the origin of this picture (pdf)

[Update: another plagiarism detected on 2014/12/29; This post originated from Grégory Favre news on the excellent EPFL Infodoc mailing list, and concerns to EPFL papers]

The pressure of publication pushes back the frontiers of laziness. Here, a sole change in a paper title allows the paper to pass through reviews (if there are any reviews in this case, look at Nuit Blanche on peer review).

If you steal from one author it's plagiarism; if you steal from many it's research. (attributed to Wilson Mizner)

The most interesting example i had seen so far was a paper i reviewed on nonsubsampled contourlets (a kind of discretized, directional wavelet). It was entitled "A New Image Denoising Scheme using the Nonsubsampled Contourlet Transform", and  submitted in 2008 to Signal Processing by three authors from one of the two most populated countries in the world. Its content had about 60% overlap with a more standard and authoritative paper on the topic. A big difference resided in the typeset: the text was written with word (instead of LaTeX), the figures were drawn in Word too (instead of Xfig, InkScape). I hereby provide a little excerpt, so you can check the subtle differences:

Original paper: 2) Nonsubsampled Directional Filter Bank (NSDFB): The directional filter bank of Bamberger and Smith [18] is constructed by combining critically-sampled two-channel fan filter banks and resampling operations. The result is a tree-structured filter bank that splits the 2-D frequency plane into directional wedges. A shift-invariant directional expansion is obtained with a nonsubsampled DFB (NSDFB). The NSDFB is constructed by eliminating the downsamplers and upsamplers in the DFB (see also [20]). This is done by switching off the downsamplers/upsamplers in each two-channel filter bank in the DFB tree structure and upsampling the filters accordingly. This results in a tree composed of two-channel NSFBs. Fig. 3 illustrates a four channel decomposition. 

Submitted paper: b: Nonsubsampled Directional Filter Bank (NSDFB) The directional filter bank of Bamberger and Smith [14] is constructed by combining critically-sampled two-channel fan filter banks and resampling operations. The result is a tree-structured filter bank that splits the 2-D frequency plane into directional wedges. A shift-invariant directional expansion is obtained with a nonsubsampled DFB (NSDFB). The NSDFB is constructed by eliminating the downsamplers and upsamplers in the DFB. This is done by switching off the downsamplers/upsamplers in each two-channel filter bank in the DFB tree structure and upsampling the filters accordingly. This results in a tree composed of two-channel Nonsubsampled Filter Banks (NSFB). Fig. 3 illustrates a four channel decomposition.

But i am very unfair: the reference list was quite different. Interestingly, to the genuine honesty of the (submitting) authors, the partly copied paper EVEN cited the original paper: Arthur L. Cunha, Jianping Zhou, Minh N. Do. The nonsubsampled contourlet transform: Theory, design, and applications. IEEE Trans. on Image processing, 2006, 15(10): 3089-3101. The paper was subsequently rejected. But (i just discovered it today, 2014/12/29), that in 2011, a paper intitled "Performance Analysis of Modified Nonsubsampled Contourlet Transform for Image Denoising" was published in the Research Journal of Applied Science, Engineering and Technology. It was written by two authors from the other of the two most populated countries in the world.

It was received: March 16, 2011, accepted: May 18, 2011 and published: July 25, 2011. That's a fast track. And it possesses many cut-caste-plagiarized parts taken from A. L. da Cunha 2006 paper, as i show below, only from the introduction:

• original: Another important feature of a transform is its stability with respect to shifts of the input signal.
• pasted: Another important feature of a transform is its stability with respect to shifts of the input signal.
• original: Thus, most state-of-the-art wavelet denoising algorithms (see for example [6]–[8]) use an expansion with less shift sensitivity than the standard maximally decimated wavelet decomposition—the most common being the nonsubsampled wavelet transform (NSWT) computed with the à trous algorithm [9].
• pasted: Thus, most state-of-the-art wavelet denoising algorithms (Chang, 2000) use an expansion with less shift sensitivity than the standard maximally decimated wavelet decomposition the most common being the nonsubsampled wavelet transform (NSWT) computed with a trous algorithm (Shensa, 1992) now it is implemented using Mat lab software
• original: In addition to shift-invariance, it has been recognized that an efficient image representation has to account for the geometrical structure pervasive in natural scenes. In this direction, several representation schemes have recently been proposed [10]–[15]. 
• pasted: In addition to shift-invariance, it has been recognized that an efficient image representation has to account for the geometrical structure pervasive in natural scenes. In this direction, several representation schemes have recently been proposed (Donoho, 1999). 
• original: In this paper, we propose an overcomplete transform that we call the nonsubsampled contourlet transform (NSCT). Our main motivation is to construct a flexible and efficient transform targeting applications where redundancy is not a major issue (e.g., denoising). The NSCT is a fully shift-invariant, multiscale, and multidirection expansion that has a fast implementation. The proposed construction leads to a filter-design problem that to the best of our knowledge has not been addressed elsewhere. The design problem is much less constrained than that of contourlets. This enables us to design filters with better frequency selectivity thereby achieving better subband decomposition. Using the mapping approach we provide a framework for filter design that ensures good frequency localization in addition to having a fast implementation through ladders steps. The NSCT has proven to be very efficient in image denoising and image enhancement as we show in this paper. 
• pasted: So In this study, we propose an over complete transform that we call the modified Nonsubsampled Contourlet Transform (NSCT). Our main motivation is to construct a flexible and efficient transform targeting applications where redundancy is not a major issue (e.g., denoising). The NSCT is a fully shift-invariant, multiscale, and multidirectional expansion that has a fast implementation. The proposed construction leads to a filter-design problem that to the best of our knowledge has not been addressed elsewhere. The design problem is much less constrained than that of contourlets.This enables us to design filters with better frequency selectivity thereby achieving better subband decomposition. So the NSCT has proven to be very efficient in image denoising.So first let us see the contourlet transform and its construction.

The new authors have mostly subsampled the reference list, so to say.

I am not sure this recent "copy-paste-publish" trend deserves as much praise as Jorge Luis Borges short story: Pierre Menard, autor del Quijote.  The story narrates 20th century writer Pierre Ménard's efforts to truly re-create Cervantes' Don Quixote, beyond a mere translation, in the 17th century Spanish, sparking thoughts on authorship, imitation and appropriation (well, 60% of my words are similar here to the Wikipedia page ;) There are worse artifacts than copy indeed: "Mirrors and fatherhood are abominable because they multiply it [human kind] and extend it.(Les miroirs et la copulation sont abominables car ils multiplient le nombre des hommes)" (J. L. Borges).

The recent example did some genuine editing: the title is partly new (SOA is mainly expanded), acknowledgments have been deleted, and the references cut to item 21. That's a Catch 22.

• Interacting with the SOA-Based Internet of Things: Discovery, Query, Selection, and On-Demand Provisioning of Web Services, IEEE TRANSACTIONS ON SERVICES COMPUTING, 2010: http://www.vs.inf.ethz.ch/res/papers/dguinard-intera-2010.pdf 
• Service Oriented Architecture-Based Internet of Things: Discovery, Query, Selection, and On-Demand Provisioning of Web Services, International Journal of Computer Science and Telecommunications, 2012 http://www.ijcst.org/Volume3/Issue1/p7_3_1.pdf ([EDIT] funnily, the paper does not seem to be accessible anymore since the publication of this post. Still there is a Google Trace, and i have saved it on my drive, in case i'd like to publish a paper on SOA-based Internet of Things in a near future ;)

Click on images for a larger view. I just discover there is a Wikipedia page in Scientific plagiarism in India.

Conference: Fixing mathematical education

[Permission to link to author slides is being asked. Stay tuned, but do not expect too much] Meanwhile, check out Simon Leys (aka Pierre Rickmans) "Le studio de l'inutilité" (or The Hall of uselessness), with a special attention to Leys' talk on 8 Nov. 2005 at l'Université catholique de Louvain, with its nice quote to Flaubert: "I have always tried to live in an ivory tower; but a tide of shit is beating at its walls, threatening to undermine it."

"Modeling is a life skill" (Solomon Garfunkel)  

"To be able to use maths at a certain level, it is necessary to learn it at the next level" (Alexandre Borovik)

 On April 4h, 2012, a meeting held in IHP, Paris. Under the motto: How to fix our math education (Comment réparer l’enseignement des mathématiques ?). The main incentive was Solomon GARFUNKEL (COMAP Inc., Boston) and David MUMFORD (Brown University) paper "How to fix our math education", New York Times, August 28th, 2011. The paper was translated in French in Le Monde (14 septembre 2011) by Jean-Michel Kantor under the same title: Comment réparer l’enseignement des mathématiques ?. Motivated by some prominence of mathematics, and bad results of France in PISA benchmarks, the conference aimed at answering the following questions:

• does our education system answer the needs of newly opened areas in the scientific and technical realms?
• how do we can train citizens on the present century?

Two talks were given by Sol Garfunkel (What Mathematics Do Educated Citizens Need To Know?)  and Alexandre Borovik (What do children learn when we teach them mathematics?), chaired and translated by Jean-Michel Kantor.

Both conferences were profound, lively, though provoking and entertaining, in a different style. Sol explained the motivations behind the NYT paper: the U.S. education was local to the extreme, with highly varying levels between states, counties, and even neighborhoods. Two great 4-letter sticker acronyms (NCLB: no child left behind, under G. Bush, and RTTT: race to the top, under B. Obama) have tried, and are trying, respectively, to change this local situation, by establishing nation-wide standards. The resulting goals reside in showing that mathematics are honestly (in the meaning of the honnête homme) useful and in ensuring the availability, in the future, of mathematicians and scientists. Mathematics provide a greater ability to understand (or model) the  world: "Modeling is a life skill" (SG). Sol reminded that cellphones and MRI are as much as engineering as maths. He also pointed out how operational research, computers, statistics used to belong to math departments, and have now grown into self-owned fields. He advocated the use of real-life examples graphs through mail delivery, Voronoi cells and bisectors via *** pizza delivery from Bengladesh call centers and rain falls in Colorado. Indeed, teachers tend to provide students with answers for questions they do not ask for. Looks like the following quote, inspired by Plotin, attributed to J. Lacan:  « l’amour  est  donner  ce  qu’on  n’a  pas  à quelqu’un  qui  n’en  veut  pas ». So students (and forthcoming adults) need an ability to estimate. Maths are a necessity for survival.

Alexandre Borovik drove a useful comparison between rhythm-impaired people (because of a drunk and noisy music teacher) and people who could not understand maths. Both are survivors. He considers (following Heinrich Neuhaus "the art of piano playing") that learning is an accumulation of neurological damages, reaching a threshold level. Some of us as only survivors. In a sort of Pareto-law, he tells that 95% of the population has no ideas on how 95% of the everyday stuff works, as a follow-on to the division of labor (Adam Smith, Frederick W. Taylor). He suggests re-branding maths into a tool for personal development and spiritual enhancement. Like music, not a profession, but a personal life-style. Teachers should thus be bound to the Hippocratic oath: do not arm. Which other school (mathematics including computer science) teaches "substitution of terms", at work in simple Excel sheets that provoke bracket overload (or in French "surcharge parenthétique") when three opening brackets and cell-depending operators confuse most people. Maths should be both interesting AND difficult, remember the "Law of excessive learning of mathematics": "to be able to use maths at a certain level, it is necessary to learn it at the next level".

He finally suggests teaching math bits at certain ages: maybe basic algebraic structures at 6-9 when kids are natural question-asking machines, leaving set-theoretic abstractions for teen-age, where sex hormones drive some appeal to pure idealities.

Additional lectures:

• Sol Garfunkel 10 Improving education will require teamwork
• Algebra: In Simplest Terms - Mathematical Induction
• Alexandre Borovik: Book in progress: Shadows of the Truth: metamathematics of Elementary Mathematics (pdf)

• Why Should Anyone Study Mathematics, Timothy S. Norfolk
• What Mathematics do Elementary Education Teachers need to know?, Bret Benesh

Todays bonus: Project Gutenberg: Mathematics' Bookshelf: classic mathematics books typeset with latex, with for instance Henri Poincaré, Science and hypothesis.

Hyperbolets (on WITS: Where is the Starlet)

A new conference is born: UCCV 2013, The 1st IEEE Workshop on User-Centred Computer Vision, due in Florida, Tampa. on January 2013. It has been added to SIVA Conferences.

While the shearlets are enjoying some spread (cf. Shearlets from MIA 2012 or this paper), some of their contributors are involved in hyperbolets, or hyperbolic wavelets, closely related cousins. Here they are (as on WITS: where is the Starlet):

Hyperbolets

In short:	An example of multi-composite wavelets with hyperbolic scaling law
Etymology:	From the hyperbola (wiki entry), with a potential reference (article no available on 2011/05/26) to the parabolic scaling law of the shearlets
Origin:	Glenn R. Easley, Demetrio Labate, Vishal M. Patel: Multi-composite wavelet estimation, Proceedings of SPIE Volume 8138, Wavelets and Sparsity XIV, Aug. 2011 (local copy) Abstract: In this work, we present a new approach to image denoising by using a general representation known as wavelets with composite dilations. These representations allow for waveforms to be defined not only at various scales and locations but also at various orientations. For this talk, we present many new representations such as hyperbolets and propose combining multiple estimates from various representations to form a unique denoised image. In particular, we can take advantage of different representations to sparsely represent important features such as edges and texture independently and then use these estimates to derive an improved estimate. The hyperbolet construction is further refined in: G. R. Easley, D. Labate and V. M. Patel, Hyperbolic shearlets, IEEE International Conference on Image Processing (ICIP), Orlando, FL, 2012, submitted (local copy) G. R. Easley, D. Labate, and V. M. Patel, Directional multiscale processing of images using wavelets with composite dilations, submitted 2011 (local copy)
Contributors:	Glenn R. Easley (no personal page), Demetrio Labate, Vishal M. Patel
Some properties:	Tiling of the frequency domain associated with an hyperbolic system of wavelets with composite dilations. Closely related to shearlets
Anecdote:
Usage:
See also:	The above work might be related to Glenn R. Easley, Demetrio Labate: Critically Sampled Wavelets with Composite Dilations (local copy), preprint, 2011, which develops interesting critically sampled directional wavelet schemes (DWTShear, CShear, QDWTShear)
Comments:

More on the topic:
2D wavelets: A panorama on multiscale geometric representations, intertwining spatial, directional and frequency selectivity